TEMA 4
LA DIVISIBILIDAD
LOS MÚLTIPLOS DE UN NÚMERO
Los múltiplos de un número natural son los números naturales que resultan de multiplicar ese número por otros números naturales.
Decimos que un número es múltiplo de otro si le contiene un número exacto de veces.
Múltiplo de un número natural es el resultado de multiplicar ese número por cualquier otro.
MÍNIMO COMÚN MÚLTIPLODecimos que un número es múltiplo de otro si le contiene un número exacto de veces.
Múltiplo de un número natural es el resultado de multiplicar ese número por cualquier otro.
escolar.com
sauce.pntic.mec.es
ntic.educacion.es
eltanque
PROPIEDADES DE LOS MÚLTIPLOS
ntic.educacion.es
ACTIVIDADES
ntic.educacion.es
ceip_san_tesifon
e-vocacion
thatquiz.org
genmagic
oswego.org
primarygames.co.uk
matemath.com
ntic.educacion.es
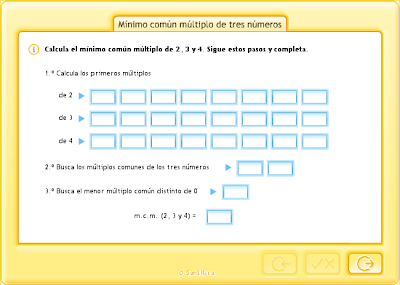
El mínimo común múltiplo (m.c.m.) es el número más pequeño, distinto de cero, que es múltiplo de dos o más números.
e-vocacion
El nombre de mínimo común múltiplo parece una contradicción, pero no es así y lo vamos a ver analizándolo.
Ya sabes que los múltiplos de un número son los resultados que tienes cuando lo multiplicas por otros números (si lo multiplicas por 1, 2, 3, 4, 5, etc.) como en las tablas de multiplicar.
¿Qué es un "múltiplo común"?
Si tienes dos (o más) números, y miras entre sus múltiplos y encuentras algunos iguales en las listas correspondientes, esos son los múltiplos comunes a los números dados.
Chabeli, María José y Manuel entrenan en el polideportivo. Chabeli va a patinaje cada 2 días, María José va a natación cada 3 días y Manuel juega al tenis cada 4 días.
¿Qué días coinciden los tres a lo largo del mes?
Para averiguarlo, vamos a calcular los días que entrena cada uno, es decir, vamos a obtener los múltiplos de 2, 3 y 4.
Los tres amigos coinciden los días 12 y 24 del mes. Observa que los números 12 y 24 son múltiplos comunes de 2, 3 y 4.
¿Qué es el "mínimo común múltiplo"?
Es simplemente el más pequeño de los múltiplos comunes.
¿Cuál es el mínimo número de días que tienen que pasar para que coincidan los tres?
Los múltiplos comunes son 12 y 24, el menor de los múltiplos comunes es 12. Por tanto, los tres amigos coinciden cada 12 días.
eltanque
ACTIVIDADES
ntic.educacion.es
ceip_san_tesifon
arquimedes.matem.unam.mx
ntic.educacion.es
ceip_san_tesifon
tinglado.net
ceip_san_tesifon
e-vocacion
olmo.pntic
odas.educarchile
LOS DIVISORES DE UN NÚMERO. NÚMEROS PRIMOS Y NÚMEROS COMPUESTOS
DIVISORES DE UN NÚMERO
Como todo número tiene sus múltiplos así también tienen sus divisores es decir otros números que lo dividen exactamente. Los divisores de un número son los que dividen a éste en forma exacta.
El uno es divisor de todos los números.
Todo número es divisor de sí mismo.
skoool.es
En el almacén, tengo cajas de todos los tamaños ¿De qué forma puedo empaquetar 12 latas de refresco en cajas iguales sin que me sobre ninguna?
Puedo agrupar las doce latas de 6 formas diferentes:
Para empaquetar las doce latas, podemos utilizar cajas de 1, 2, 3, 4, 6 y 12 unidades.
CÁLCULO DE LOS DIVISORES
Para determinar los divisores de un número, se buscan todos los números que lo dividen en forma exacta, es decir, el residuo debe ser cero.
e-vocacion
Para averiguarlo tenemos que calcular los divisores de 10, es decir, los números que dividen a 10 y dan de resto cero.
Los números 1, 2, 5 y 10 son los divisores, porque al dividir 10 entre cada uno de ellos, la división es exacta.
ACTIVIDADES
ntic.educacion.es
genmagic.org
el tanque
ceip_san_tesifon
carambolo
eltanque
ntic.educacion.es
e-ducativa.catedu.es
educarchile.cl
medusa
uco.es
NÚMEROS PRIMOS Y NÚMEROS COMPUESTOS
El número 5 solo tiene dos divisores, el 1 y el 5.
Los números que sólo tienen dos divisores se llaman números primos.
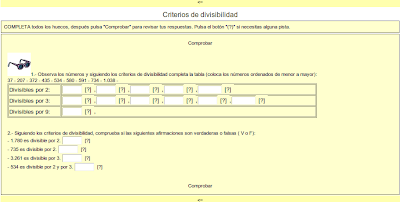
CRITERIOS DE DIVISIBILIDAD
Para saber si un número es múltiplo de otro, o si éste es divisor de aquel, podéis aprender los criterios de divisibilidad y ahorraros muchísimas divisiones.
Criterio de divisibilidad por 2: Un número es divisible por 2, si termina en cero o cifra par.
24, 238, 1024.
Criterio de divisibilidad por 3: Un número es divisible por 3, si la suma de sus dígitos nos da múltiplo de 3.
564: 5 + 6 + 4 = 15, es mútiplo de 3
2040: 2 + 0 + 4 + 0 = 6, es mútiplo de 3
Criterio de divisibilidad por 5: Un número es divisible por 5, si termina en cero o cinco.
45, 515, 7525.
Criterio de divisibilidad por 7: Un número es divisible por 7 cuando la diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 0 ó múltiplo de 7.
343: 34 - 2 · 3 = 28, es mútiplo de 7
105: 10 - 5 · 2 = 0
2261: 226 - 1 · 2 = 224
Volvemos a repetir el proceso con 224.
22 - 4 · 2 = 14, es mútiplo de 7.
Criterio de divisibilidad por 11: Un número es divisible por 11, si la diferencia entre la suma de las cifras que ocupan los lugares pares y la de los impares es 0 ó múltiplo de 11.
121: (1 + 1) - 2 = 0
4224: (4 + 2) - (2 + 4) = 0
Otros criterios de divisibilidad
Criterio de divisibilidad por 4: Un número es divisible por 4, si sus dos últimas cifras son ceros o múltiplo de 4.
36, 400, 1028.
Criterio de divisibilidad por 6: Un número es divisible por 6, si es divisible por 2 y por 3.
72, 324, 2 400
Criterio de divisibilidad por 8: Un número es divisible por 8, si sus tres últimas cifras son ceros o múltiplo de 8.
4000, 1048, 1512.
Criterio de divisibilidad por 9: Un número es divisible por 9, si la suma de sus dígitos nos da múltiplo de 9.
81: 8 + 1 = 9
3663: 3 + 6 + 6 + 3 = 18, es mútiplo de 9
Criterio de divisibilidad por 25: Un número es divisible por 25, si sus dos últimas cifras son ceros o múltiplo de 25.
500, 1025, 1875.
Criterio de divisibilidad por 125: Un número es divisible por 125, si sus tres últimas cifras son ceros o múltiplo de 125.
1000, 1 125, 4 250.
Rarezas de la divisibilidad:
Cualquier número de 3 cifras iguales es divisible por 37, porque 111 es divisible por 37.
Cualquier número de 4 cifras iguales es divisible por 11, porque 1111 es divisible por 11.
Cualquier número de tres cifras como 697 ampliado por repetición de sus cifras 697697, siempre será divisible por 7, 11 y 13.
Lo mismo que un número de cuatro cifras 7538 ampliado por repetición de las sus cifras, 75385387, siempre será divisible por 73 y por 137.
Divisibilidad por 13:
Elimina el último dígito del número dado; a continuación resta nueve veces ese dígito al número obtenido. Si el resultado es divisible por 13, también lo es el número original. (Esta regla es recurrente; puede usarse sucesivamente tantas veces como se quiera hasta obtener un número que sepamos que es divisible por 13).
Ejemplo: 16312179
1631217 – (9x9) = 1631136
163113 – (6x9) = 163059
16305 – (9x9) = 16224
1622 – (4x9) = 1586
158 – (6x9) = 104. Como sabemos que 104 (13×8=104) es divisible por 13, 16312179 también lo es.
CRITERIOS DE DIVISIBILIDAD
Criterio de divisibilidad por 2: Un número es divisible por 2, si termina en cero o cifra par.
24, 238, 1024.
Criterio de divisibilidad por 3: Un número es divisible por 3, si la suma de sus dígitos nos da múltiplo de 3.
564: 5 + 6 + 4 = 15, es mútiplo de 3
2040: 2 + 0 + 4 + 0 = 6, es mútiplo de 3
Criterio de divisibilidad por 5: Un número es divisible por 5, si termina en cero o cinco.
45, 515, 7525.
Criterio de divisibilidad por 7: Un número es divisible por 7 cuando la diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 0 ó múltiplo de 7.
343: 34 - 2 · 3 = 28, es mútiplo de 7
105: 10 - 5 · 2 = 0
2261: 226 - 1 · 2 = 224
Volvemos a repetir el proceso con 224.
22 - 4 · 2 = 14, es mútiplo de 7.
Criterio de divisibilidad por 10: un número es divisible por 10, si la cifra de las unidades es 0.
130, 1440, 10 230
121: (1 + 1) - 2 = 0
4224: (4 + 2) - (2 + 4) = 0
Otros criterios de divisibilidad
Criterio de divisibilidad por 4: Un número es divisible por 4, si sus dos últimas cifras son ceros o múltiplo de 4.
36, 400, 1028.
Criterio de divisibilidad por 6: Un número es divisible por 6, si es divisible por 2 y por 3.
72, 324, 2 400
Criterio de divisibilidad por 8: Un número es divisible por 8, si sus tres últimas cifras son ceros o múltiplo de 8.
4000, 1048, 1512.
Criterio de divisibilidad por 9: Un número es divisible por 9, si la suma de sus dígitos nos da múltiplo de 9.
81: 8 + 1 = 9
3663: 3 + 6 + 6 + 3 = 18, es mútiplo de 9
Criterio de divisibilidad por 25: Un número es divisible por 25, si sus dos últimas cifras son ceros o múltiplo de 25.
500, 1025, 1875.
Criterio de divisibilidad por 125: Un número es divisible por 125, si sus tres últimas cifras son ceros o múltiplo de 125.
1000, 1 125, 4 250.
Rarezas de la divisibilidad:
Cualquier número de 3 cifras iguales es divisible por 37, porque 111 es divisible por 37.
Cualquier número de 4 cifras iguales es divisible por 11, porque 1111 es divisible por 11.
Cualquier número de tres cifras como 697 ampliado por repetición de sus cifras 697697, siempre será divisible por 7, 11 y 13.
Lo mismo que un número de cuatro cifras 7538 ampliado por repetición de las sus cifras, 75385387, siempre será divisible por 73 y por 137.
Divisibilidad por 13:
Elimina el último dígito del número dado; a continuación resta nueve veces ese dígito al número obtenido. Si el resultado es divisible por 13, también lo es el número original. (Esta regla es recurrente; puede usarse sucesivamente tantas veces como se quiera hasta obtener un número que sepamos que es divisible por 13).
Ejemplo: 16312179
1631217 – (9x9) = 1631136
163113 – (6x9) = 163059
16305 – (9x9) = 16224
1622 – (4x9) = 1586
158 – (6x9) = 104. Como sabemos que 104 (13×8=104) es divisible por 13, 16312179 también lo es.
ACTIVIDADES
eltanque
ntic.educacion.es
anaya
recursostic.educacion
e-vocacion
genmagic
eltanque
genmagic.org
carambolo
odas.educarchile
TEMA 3
POTENCIAS Y RAÍZ CUADRADA
LAS POTENCIAS
INTRODUCCIÓN A LAS POTENCIAS
ceibal.edu.uy
POTENCIA
ceibal.edu.uy
ntic.educacion.es
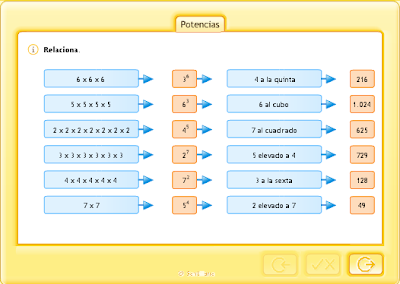
Una potencia es la forma corta de expresar un producto de factores iguales.
iesberlanga.org
e-vocacion
sauce.pntic.mec.es
eltanque
anaya
Potencias en la vida cotidiana
e-vocacion
LECTURA DE POTENCIAS
ntic.educacion.es
ACTIVIDADES
recursostic.educacion
e-vocacion
ceip_san_tesifon
genmagic.net
librosvivos.net
anaya
eltanque
anaya
ntic.educacion.es
escritorioalumnos.educ.ar
ceibal.edu.uy
POTENCIAS DE BASE 10
Una potencia de base 10 se utiliza para representar números como el 100, 1000, 10000 ... y se calcula tomando la unidad seguida de tantos ceros como indique el exponente.
iesberlanga.org
ceibal.edu.uy
eltanque
ACTIVIDADES
genmagic.net
e-vocacion
e-vocacion.es
anaya
e-vocacion
ceip_san_tesifon
ceibal.edu.uy
genmagic.net
DE LO PEQUEÑO A LO GRANDE (Y VICEVERSA)
wisphysics.es
nanoreisen.de
eltanque
anaya
e-vocacion
thatquiz.org
eltanque
catedu.es
anaya
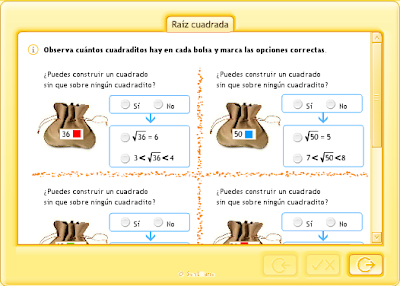
LA RAÍZ CUADRADA Y LA CALCULADORA
agrega.educa.madrid
platea.pntic.mec.es
TEMA 2
LA SUMA Y LA RESTA. PROPIEDADES
LA SUMA Y LA RESTA. PROPIEDADES
LA SUMA
disfrutalasmatematicas
LA RESTA
disfrutalasmatematicas
- Términos de la resta
sauce.pntic.mec.es
descartes
PROPIEDADES DE LA SUMA Y LA RESTA
- Propiedad conmutativa de la suma
mathematicsdictionary
- Propiedad asociativa de la suma
mathematicsdictionary
- Propiedad fundamental de la resta
descartes
- Relaciones de la suma y la resta
salonhogar
ACTIVIDADES
polavide
ies/pravia
educacyl
carambolo
polavide
educastur
educacyl
eltanque
i-matematicas.com
supersaber
descartes
iboard
proyectoagrega
genmagic.net
editorialteide.es
carambolo
LA MULTIPLICACIÓN. PRÁCTICA Y PROPIEDADES
LA MULTIPLICACIÓN
MULTIPLICACIÓN DE UN NÚMERO POR OTRO DE VARIAS CIFRAS
librosvivos.net
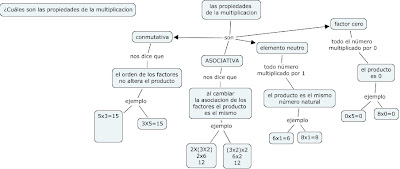
PROPIEDADES DE LA MULTIPLICACIÓN
roble.pntic.mec.es
ACTIVIDADES
eltanque
genmagic
ntic.educacion.es
polavide
ies/pravia
juntadeandalucia/averroes
educacyl
eltanque
cpantoniodeulloa
editorialteide
descartes
didacmaticprimaria
didacmaticprimaria
dl.dropbox.com
APRENDER MÁS: ESTRATEGIAS DE LAS MULTIPLICACIONES
A continuación se muestran las estrategias que consideramos más útiles para aplicar, solas o combinadas con otras, según nos interese.
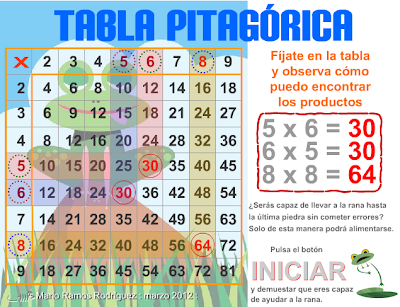
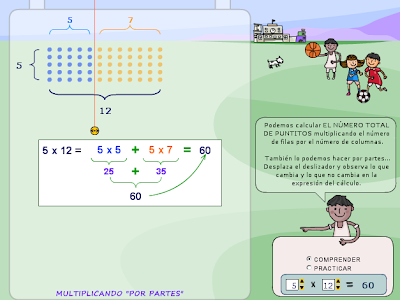
- En las multiplicaciones con varios factores es conveniente, cuando sea posible, recolocar los factores para encontrar productos más sencillos. 5 x 7 x 2 = 5 x 2 x 7 = 10 x 7 = 70
- 25 x 9 x 4 = 25 x 4 x 9 = 100 x 9 = 900
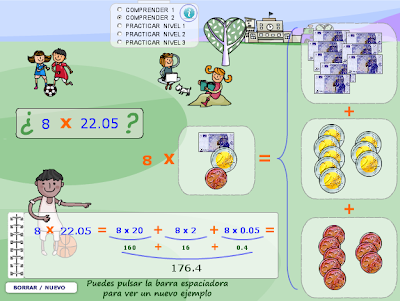
- Descomponer los factores en sumas o restas y después de hacer las multiplicaciones parciales, sumar o restar los productos obtenidos. 56 x 7 = (50 + 6) x 7 = 50 x 7 + 6 x 7 = 350 + 42 = 392
- 39 x 8 = (40 – 1) x 8 = 40 x 8 – 1 x 8 = 320 – 8 = 312
- Multiplicar un número por 5 (10 : 2) es lo mismo que multiplicar por 10 (añadir un cero al número dado) y dividir por 2 (calcular su mitad). 27 x 5 = 27 x (10 : 2) = 270 : 2 = 135
- 483 x 5 = 483 x (10 : 2) = 4830 : 2 = 2415
- La multiplicación por 5, también puede hacerse calculando primero la mitad del número dado (dividir por 2) y después añadir un cero (multiplicar por 10).
- 28 x 5 = (28 : 2) x 10 = 14 x 10 = 140
- 356 x 5 = (356 : 2) x 10 = 178 x 10 = 1780
- Multiplicar un número por 9 (10-1) es lo mismo que multiplicar por 10 (añadir un cero) y restar el número. 78 x 9 = 78 x 10 - 78 = 780 - 78 = 702
- 125 x 9 = 125 x 10 - 125 = 1250 - 125 = 1125
- Para multiplicar un número de dos cifras por 11 podemos aplicar una estrategia interesante. Supongamos que nos piden calcular 62 x 11. Para ello imaginamos el número dejando un espacio entre los dos dígitos (6 ___ 2), y en ese espacio ponemos la suma de los dos dígitos (6+2=8). Por tanto 62 x 11 = 682. 34 x 11 = 3 ( 3+4 ) 4 = 374
- 53 x 11 = 5 ( 5+3 ) 3 = 583
- Si la suma de los dos dígitos es mayor de 9, por ejemplo en el caso de 75 x 11 = 7 7+5 5 = 7 12 5 (dejamos el 2 en el espacio en blanco, y el 1 lo sumamos al 7) = (7+1) 2 5 = 825.
- 89 x 11 = 8 ( 8+9 ) 9 = 8 17 9 = (8+1) 7 9 = 979
- 56 x 11 = 5 ( 5+6 ) 6 = 5 11 6 = (5+1) 1 6 = 616
- Para multiplicar un número de más de dos cifras por 11, el procedimiento es parecido al anterior. Los números de las esquinas se quedan igual, y en el centro vamos poniendo las sumas de los pares de números adyacentes. 234 x 11 = 2 ( 2+3 ) ( 3+4 ) 4 = 2574
- 5324 x 11 = 5 ( 5+3 ) ( 3+2 ) ( 2+4 ) 4 = 58564
- Si alguna de las sumas es mayor de 9 (de dos cifras), escribimos el dígito de las unidades y el 1 lo sumamos al número de la izquierda. 348 x 11 = 3( 3+4 )( 4+8 )8 = 3(7)(12)8 = 3(7+1)28 = 3828
- 763 x 11 = 7( 7+6 )( 6+3 )3 = 7(13)(9)3 = (7+1)393 = 8393
- Multiplicar un número por 12 (10+2) es lo mismo que multiplicar el número por 10 (añadir un cero) y sumar el doble del número (multiplicarlo por 2). 8 x 12 = 8 x (10+2) = (8x10) + (8x2) = 80 + 16 = 96
- 35 x 12 = 35 x (10+2) = (35x10) + (35x2) = 350 + 70 = 420
- Multiplicar un número por 15 (10+5) es lo mismo que multiplicar el número por 10 (añadir un cero) y sumar la mitad de la multiplicación anterior. 7 x 15 = (7 x 10) + (7 x 5) = 70 + 35 = 105
- 48 x 15 = (48 x 10) + (48 x 5) = 480 + 240 = 720
- Para multiplicar números de dos cifras inferiores a 20, podemos aplicar un truco que parece complicado pero da buenos resultados. Por ejemplo, para multiplicar 18 x 14, procedemos como sigue:
- - Al primer número se suman las unidades del segundo: (18 + 4 = 22) y lo multiplicamos por 10, (añadimos un 0): 220
- - A este resultado se le suma el producto de las unidades de los números: (8 x 4) = 32 y nos queda 220 + 32 = 252.
- 12 x 16 = (12 + 6) x 10 + (2 x 6) = 180 + 12 = 192
- 13 x 17 = (13 + 7) x 10 + (3 x 7) = 200 + 21 = 221
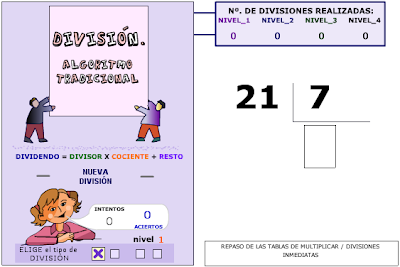
PRÁCTICA DE LA DIVISIÓN
disfrutalasmatematicas
e-vocacion.es
TÉRMINOS DE LA DIVISIÓN
sauce.pntic.mec.es
ESTIMACIÓN DE COCIENTES
carambolo
PROPIEDAD FUNDAMENTAL DE LA DIVISIÓN
Para repasar esta propiedad, pincha en la imagen.
box.net
DIVISIÓN CON CEROS EN EL COCIENTE
Para recordar, pincha en la imagen.
RELACIÓN ENTRE PRODUCTO Y DIVISIÓN
carambolo
ACTIVIDADES
ntic.educacion.es
cuadernosdigitalesvindel.com
eltanque
eltanque
genmagic.net
ies/pravia
anaya
juntadeandalucia.es/averroes
eltanque
agrega.hezkuntza.net
librosvivos.net
LA JERARQUÍA DE LAS OPERACIONES COMBINADAS
ACTIVIDADES
recursostic.educacion.es
ceipchanopinheiro
i-matematicas.com
ceip_san_tesifon
genmagic.net
medusa
ceibal.edu.uy
e-vocacion.es
cprejea.educa.aragon.es
TEMA 1
Donald en el país de las matemáticas
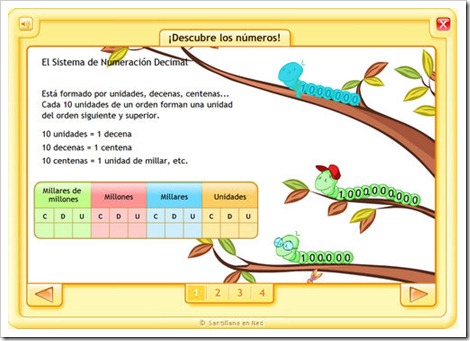
NUESTRO SISTEMA DE NUMERACIÓN DECIMAL
roble.pntic.mec.es
agrega.educa.madrid.org
web.educastur.princast.es
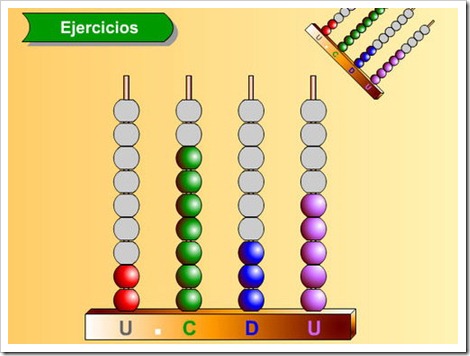
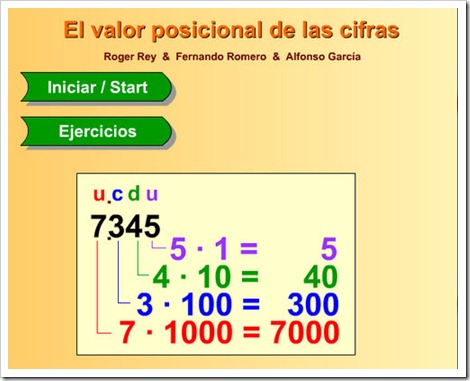
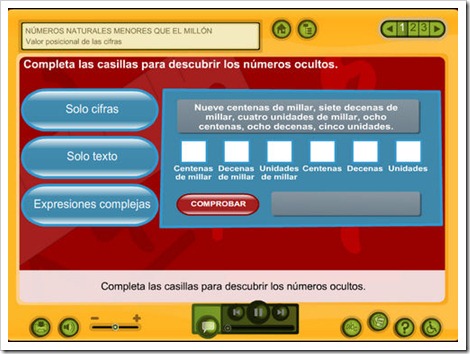
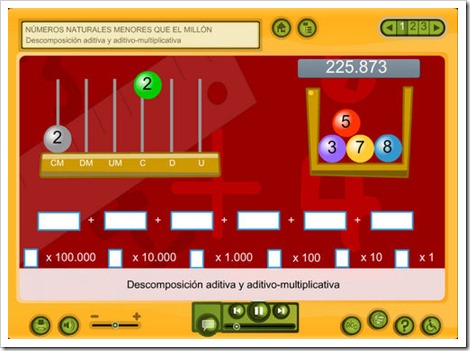
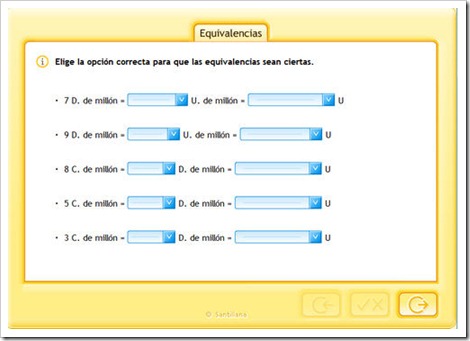
Orden de unidades y valor posicional
contenidos.santillanaenred.com
genmagic.net
genmagic.net
agrega.educa.madrid.org
agrega.educa.madrid.org
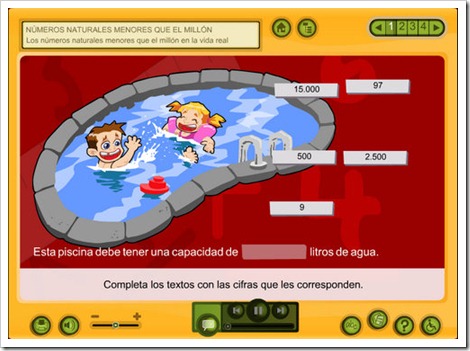
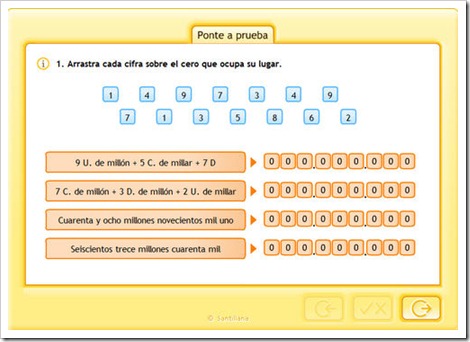
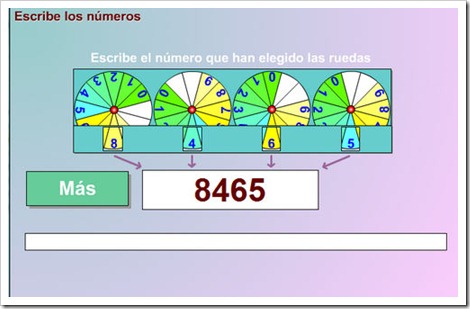
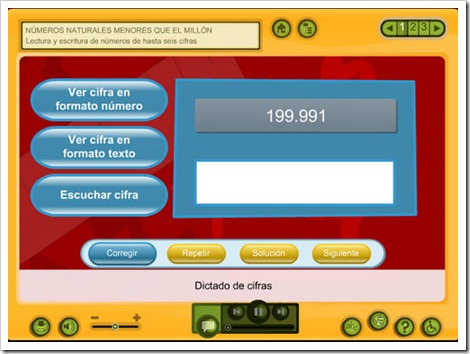
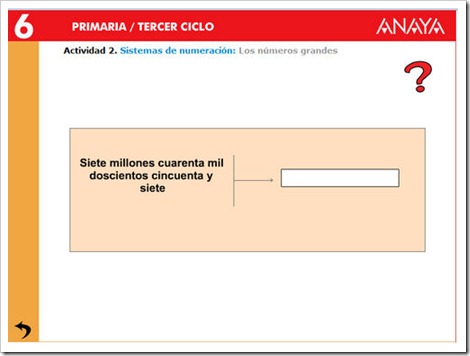
Lectura, escritura y descomposición
agrega.educa.madrid.org
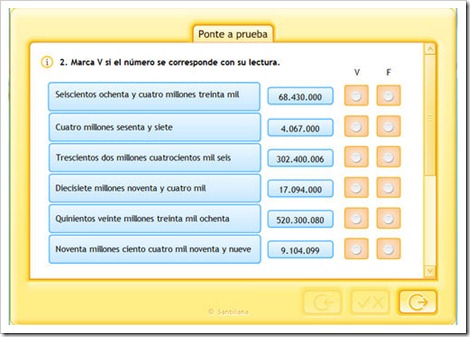
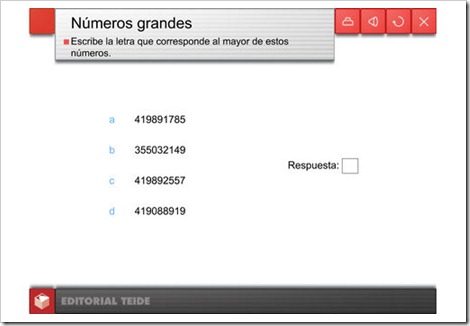
LOS NÚMEROS GRANDES
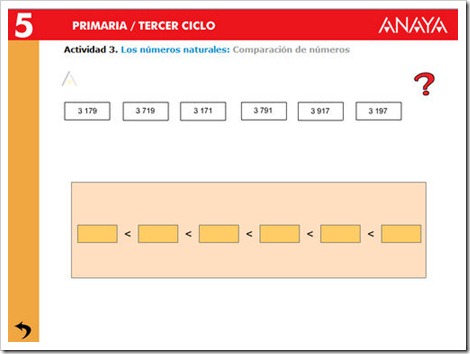
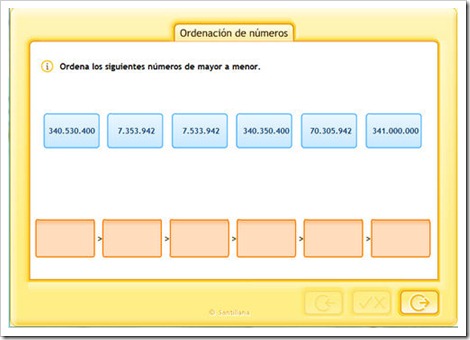
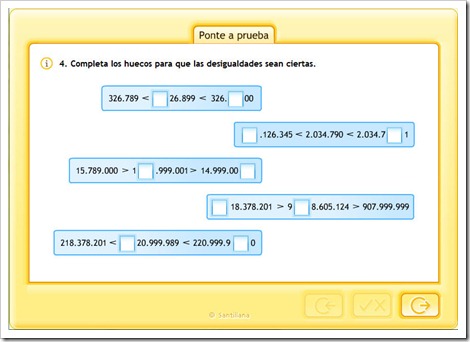
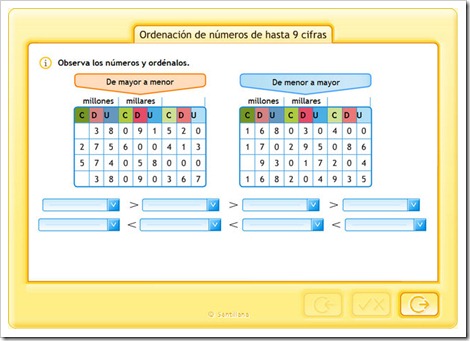
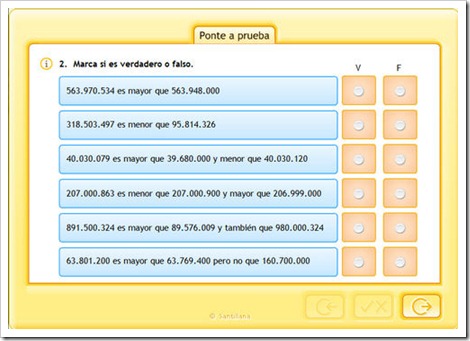
ORDEN Y COMPARACIÓN
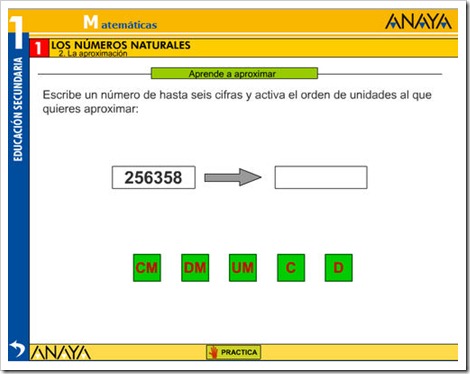
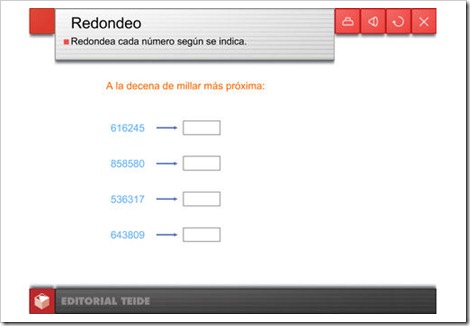
APROXIMACIÓN
web.educastur.princast.es
RELACIONES DE CLASIFICACIÓN Y ORDEN
grega.educa.madrid.org
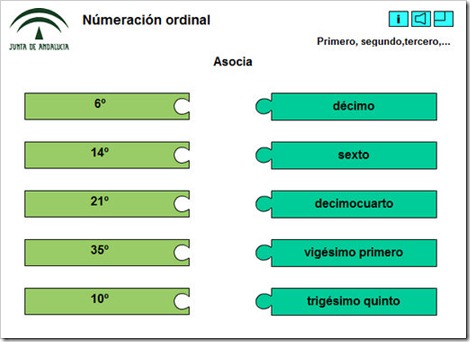
LOS NÚMEROS ORDINALES
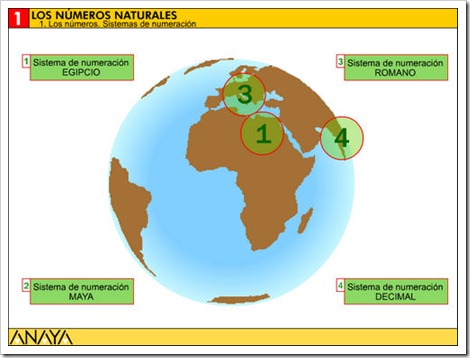
LA NUMERACIÓN ROMANA
TEMA 13
CUERPOS GEOMÉTRICOS.VOLUMEN
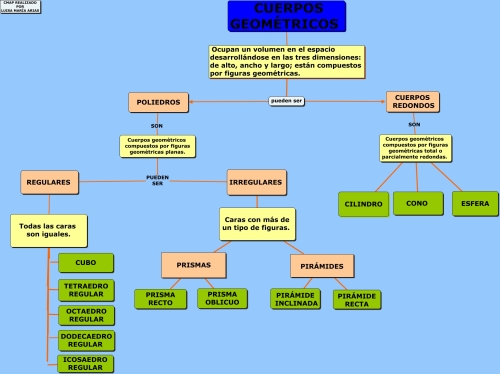
CUERPOS GEOMÉTRICOS.MAPA CONCEPTUAL
cmapspublic2.ihmc.us/
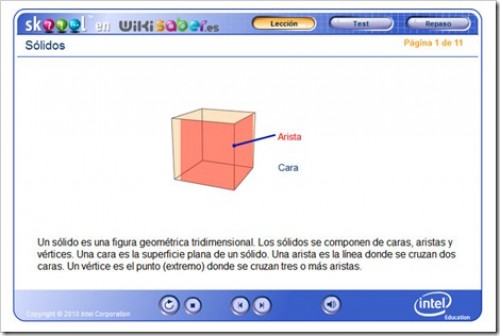
¿QUÉ SON LOS CUERPOS GEOMÉTRICOS?
www.escueladigital.com.uy
¿QUÉ SON LOS CUERPOS GEOMÉTRICOS?. CLASES Y ACTIVIDADES
cplosangeles.juntaextremadura.net
JUEGO DE LAS CONSTRUCCIONES
contenidos.santillanaenred.com
ELEMENTOS DE LOS CUERPOS GEOMÉTRICOS
www.wikisaber.es
/www.skoool.es
www.e-vocacion.es
genmagic.net
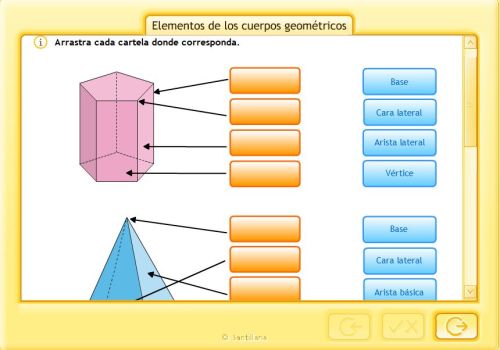
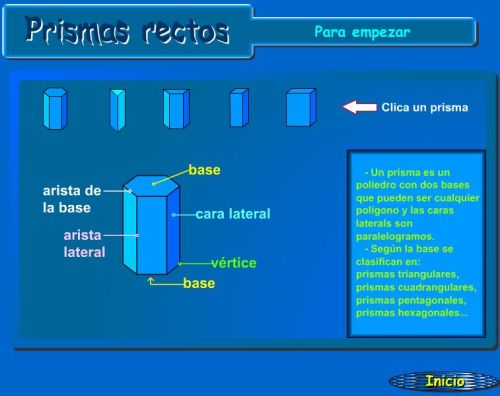
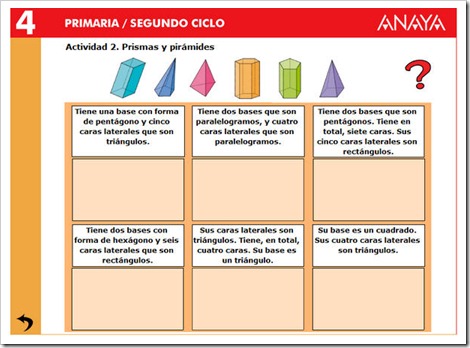
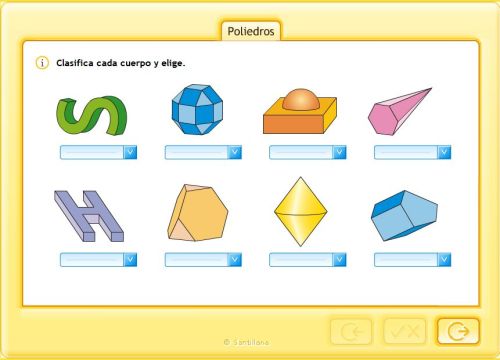
CLASIFICACIÓN DE LOS POLIEDROS
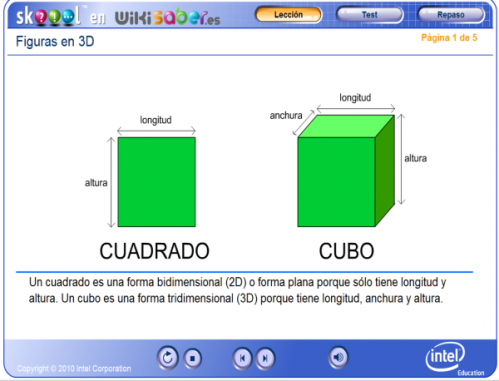
Son cuerpos geométricos cuyas caras son polígonos.
View more presentations from claudiabsimon
¿son prismas o pirámides?
/www.ceipjuanherreraalcausa.es
www.primaria.librosvivos.net
¿son poliedros o no?
www.e-vocacion.es
www.ceibal.edu.uy
JUEGO
CLASES DE CUERPOS GEOMÉTRICOS Y ELEMENTOS
www.primaria.librosvivos.net
www.primaria.librosvivos.net
TEMA 12
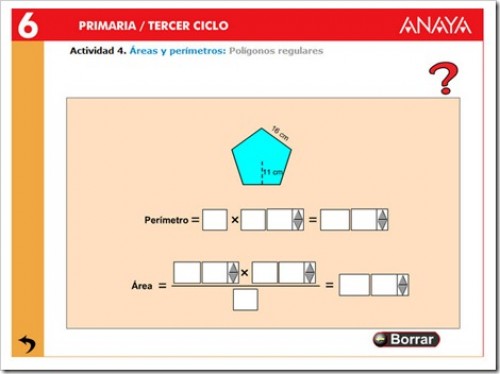
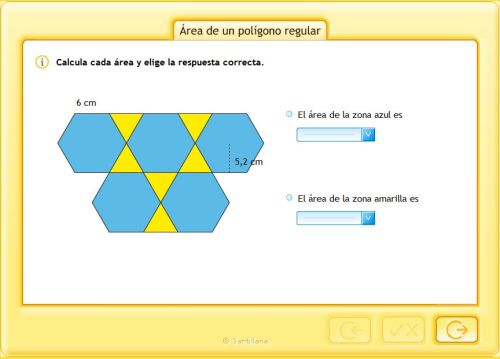
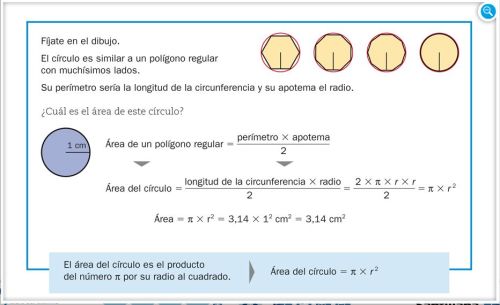
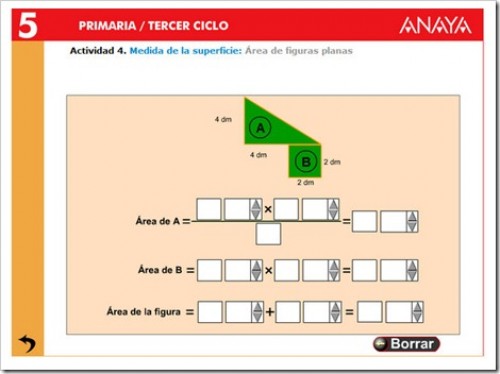
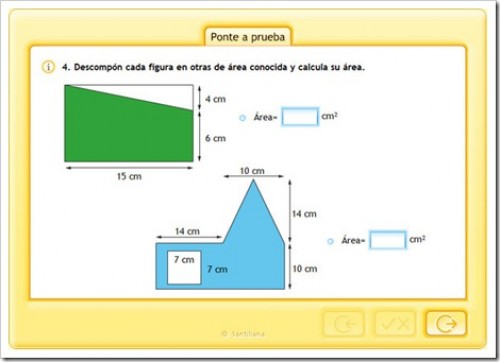
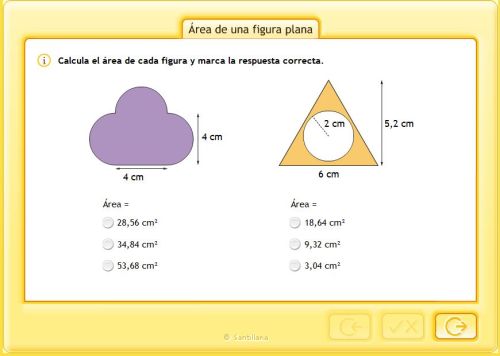
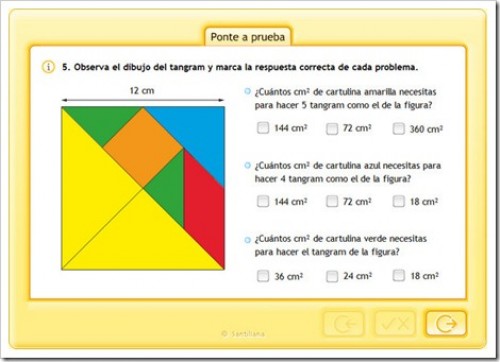
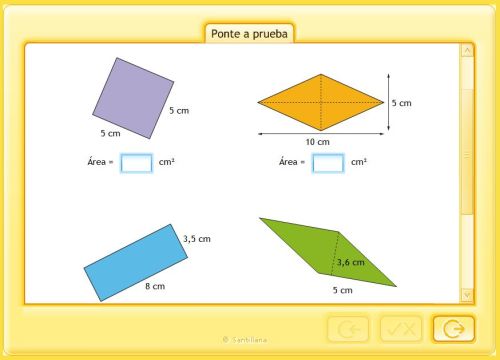
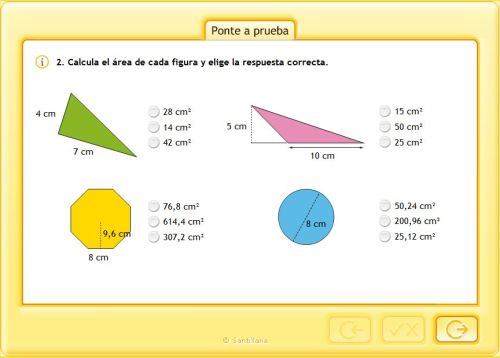
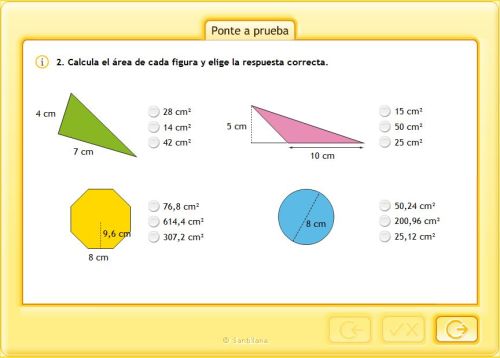
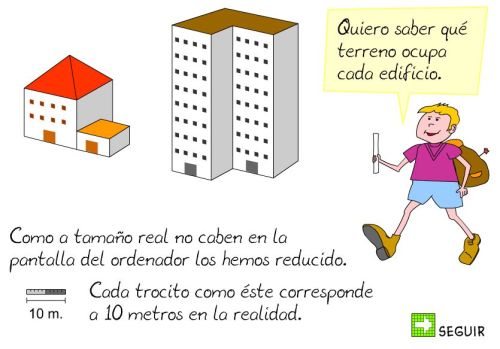
ÁREAS Y PERÍMETROS
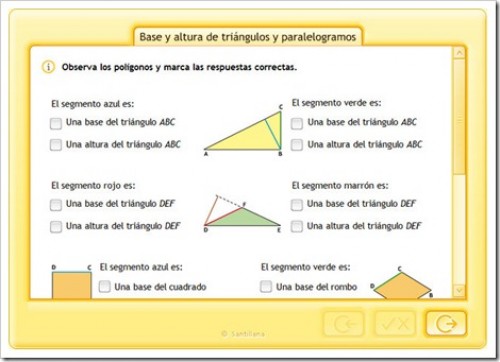
REPASAMOS LAS BASES Y LAS ALTURAS DE LOS PARALELOGRAMOS Y TRIÁNGULOS
/www.e-vocacion.es
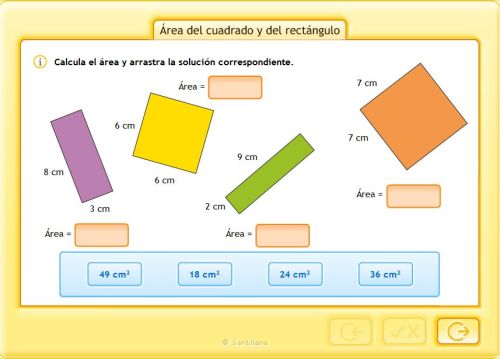
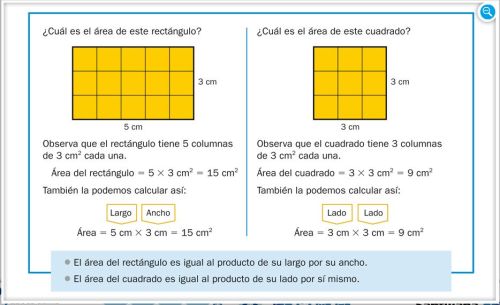
APRENDEMOS A CALCULAR EL ÁREA DEL CUADRADO Y DEL RECTÁNGULO
ÁREA DEL RECTÁNGULO Y CUADRADO
genmagic.org/mates1
www.e-vocacion.es
PROBLEMAS CON CUADRADOS Y RECTÁNGULOS
- .e-vocacion.es/
ÁREA DEL ROMBO
.e-vocacion.es
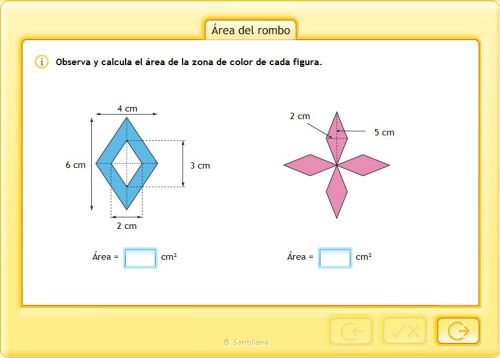
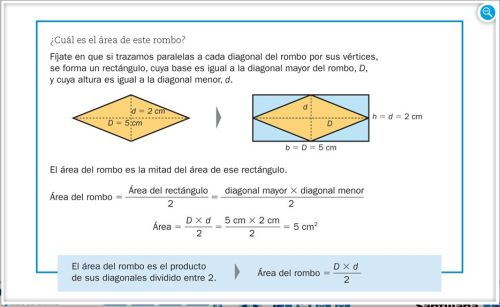
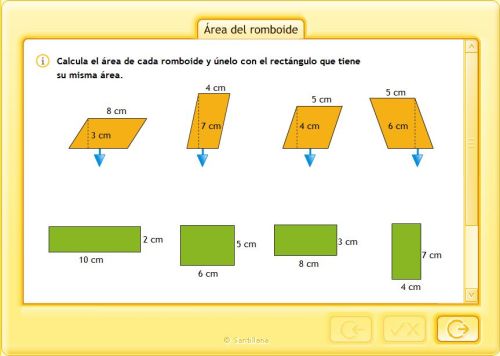
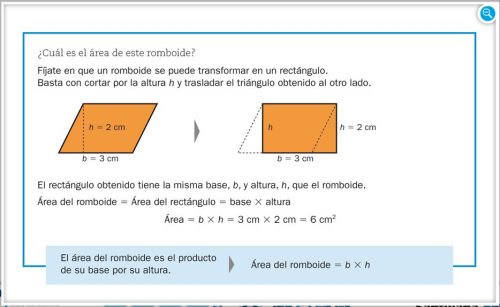
ÁREA DEL ROMBOIDE
www.e-vocacion.es
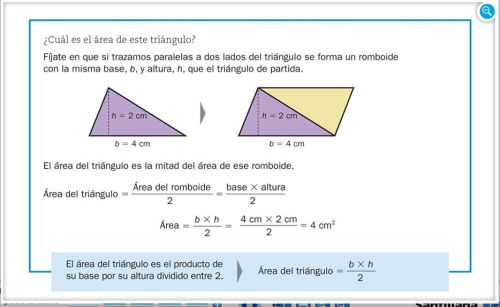
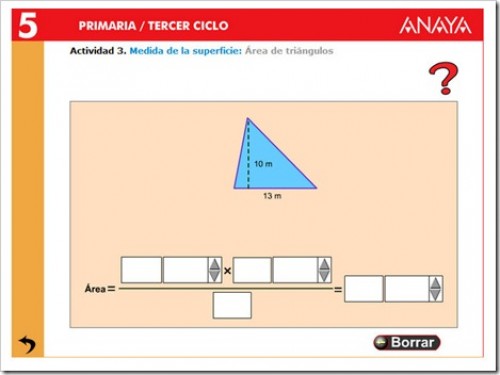
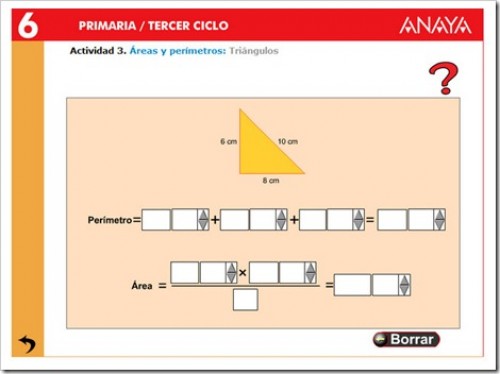
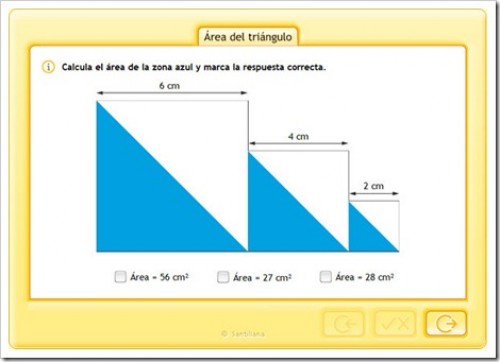
ÁREA DEL TRIÁNGULO
new_media
e-vocación
www.ceipjuanherreraalcausa.es
www.ceipjuanherreraalcausa.es
ÁREA DE LOS POLÍGONOS REGULARES
www.e-vocacion.es
/www.ceipjuanherreraalcausa.es
www.e-vocacion.es
www.e-vocacion.es
www.e-vocacion.es
www.educa.madrid.org
ÁREA DE UNA FIGURA PLANA
www.e-vocacion.es
www.e-vocacion.es
www.ceipjuanherreraalcausa.es
www.e-vocacion.es
www.e-vocacion.es
www.e-vocacion.es
www.e-vocacion.es
www.e-vocacion.es
www.e-vocacion.es
www.e-vocacion.es
REPASA LAS ÁREAS
cplosangeles.juntaextremadura.net
ELIGE EL EDIFICIO QUE TÚ QUIERAS Y MÍDELO CON LA REGLA VIRTUAL
/ntic.educacion.e
TEMA 11
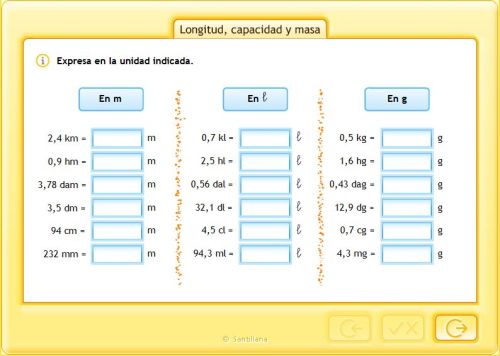
MEDIDAS DE LONGITUDES Y SUPERFICIES
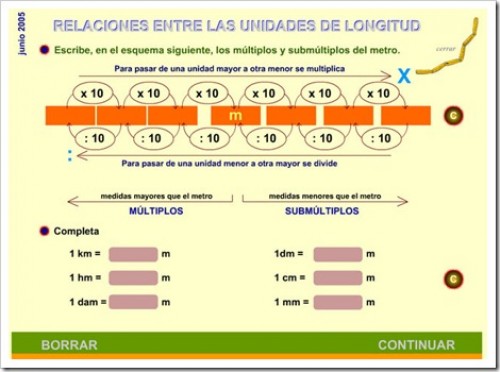
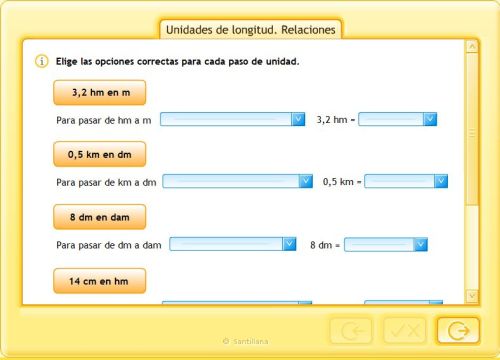
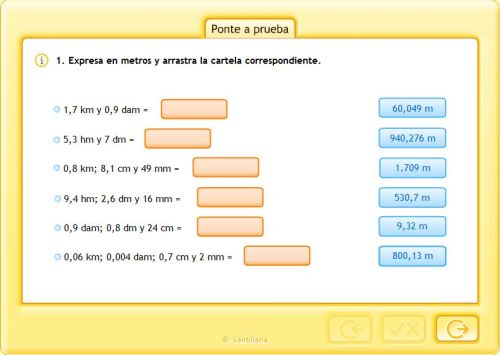
SISTEMA MÉTRICO DECIMAL
www.conevyt.org.mx
www.e-vocacion.es
APRÉNDELO TÚ MISMO/A
www.e-vocacion.es
www.e-vocacion.es
COMPRUEBA LO QUE SABES
www2.gobiernodecanarias.org
TEMA 10
ÁNGULOS. CLASES Y MEDIDAS
Tipos de ángulos (II)
Ángulos complementarios y suplementarios
Calcula los ángulos
Unidades de medida
Sistema sexagesimal
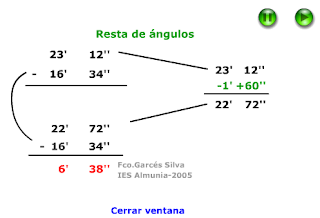
Operaciones con ángulos
Ángulos complementarios y suplementarios
Calcula los ángulos
Unidades de medida
Sistema sexagesimal
Operaciones con ángulos
LOS NÚMEROS DECIMALES
-
Suma de números decimales
-
Suma de decimales
-
Suma de decimales II
-
Resta de decimales
-
Resta de decimales II
-
Suma y resta de decimales
-
Suma y resta de decimales II
-
Suma y resta de decimales III
-
Suma y resta de decimales IV
-
Multiplicar decimales
-
Multiplicación de decimales
-
Multiplicar decimales
-
Multiplicar por la unidad seguida de ceros
-
Multiplicar por la unidad seguida de ceros II
-
Multiplicación de decimales
-
Dividir por la unidad seguida de ceros
-
Dividir por la unidad seguida de ceros
-
Multiplicación y división por la unidad seguida de ceros
-
Operaciones con decimales
Unidad 8: Números decimales. Operaciones
|
Web interactivas
|
Jclic
|
Suma y resta de números decimales
|
||
Multiplicación de números decimales
|
||
Aproximación de números decimales
|
||
Estimaciones
|
||
Multiplicar un número natural por 2
|
||
Multiplicar un número natural por 5
|
||
P: Anticipar una solución aproximada
|
RESUELVE PROBLEMAS (SM Ud. 2)
|
|
|
(SM Ud. 2)
|
NÚMEROS POSITIVOS Y NEGATIVOS
1. TRONCHO Y PONCHO
2. EL ASCENSOR
3. ALTURAS CON NÚMEROS ENTEROS
4.EL TERMÓMETRO
5.LA RECTA ENTERA
7.SUMA DE UN ENTERO POSITIVO
8.SUMA DE UN ENTERO NEGATIVO
MÚLTIPLOS Y DIVISORES
Introducción a los múltiplos.Múltiplos de un número(m.c.m.)
Cálculo de múltiplos.
Busca en la noche los múltiplos
m.c.m. de varios números
Propiedades de los múltiplos
Divisores de un número
Reglas de la divisibilidad
